A thin thread of viscous fluid falling onto a moving belt generates a surprising variety of patterns depending on the belt speed, fall height, flow rate, and fluid properties. Here, we simulate this experiment numerically using the discrete viscous threads method that can predict the non-steady dynamics of thin viscous filaments, capturing the combined effects of inertia and of deformation by stretching, bending, and twisting. Our simulations successfully reproduce nine out of ten different patterns previously seen in the laboratory and agree closely with the experimental phase diagram of Morris et al. [Phys. Rev. E 77, 066218 (2008)]. We propose a new classification of the patterns based on the Fourier spectra of the longitudinal and transverse motion of the point of contact of the thread with the belt. These frequencies appear to be locked in most cases to simple ratios of the frequency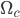 
of steady coiling obtained in the limit of zero belt speed. In particular, the intriguing “alternating loops” pattern is produced by combining the first five multiples of 
.
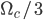The same type of thread poured on a canvass from a nozzle which follows a random trajectory one may form some patterns reminiscent of Jackson Pollock style:
