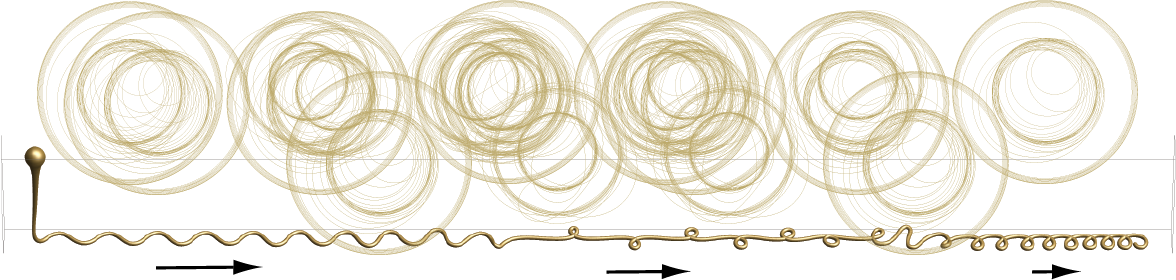
When pouring honey onto a toast one may easily  observes the formation of a coiling pattern. That very same pattern is found when a climbing rope falls onto the ground and it is not that often that elastic and viscous things behave in the same way!  It stands to reason to look for the common feature between these objects: their slenderness.

Let us quickly push the slenderness argument forward and see how it impacts the dynamics. By definition a slender  thread is tied up to its tangent 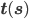 which has a norm of 1. Therefore 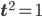so that 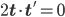where a prime denotes a derivation along the arclength 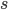. Consequently 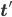is normal to the tangent. This is equivalent to writing 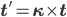where 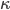is the thread's curvature. One may do the same thing deriving along with time yielding: 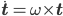. 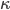and 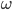are the Darboux vectors associated to the triad vector that characterize the thread.

It is to be noted that the dynamics of the thread, hence 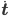, essentially induces a rotational speed be it for an elastic or a viscous rope. This a first insight on why these objects behave similarly. Their respective constitutive laws are blurred away by their geometry.

More info on the subject : DVR.